The Method of Determinants
To begin our treatment of determinant methods for solving linear systems, we would like to consult the classic text, Ars Magna, published in 1845 by scoundrelous physician and intentional curmudgeon, Girolamo Cardano.
Cardano poses the following problem.
Three men had some money. The first man with half the others' would have had $32; the second with one-third the others', $28; and the third with one-fourth the others', $31. How much had each?
From this, we get the 3 × 3 linear system
 = 32)
 = 28)
 = 31)
No, Charly, the language is not weird, its English. Yes, Charly, that's not even a lot of money for one man, nevermind three. That's not the point. Where were we? Let's get back to it, shall we? After solving the third equation for z, Cardano reduces the problem to solving the 2 × 2 linear system
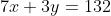
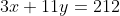
He then chooses to use the tried and true rule for four proportional quantities on the second equation to obtain the equivalent system
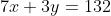
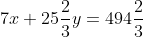
We can see what he's going to do next. He suggests this means
 = 494\frac{2}{3} - 132)
which gives us
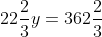
Thus, the second man's share of the money is y = $16. Using this result on the original first and second equations, he gives us the second 2 × 2 system
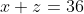
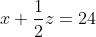
Illustrating the same technique as before, Cardano tells us that the third man's share is 24. After solving the original first equation with the knowledge that the second and third men have $16 and $24, respectively, he determines that the first man has $12. He then concludes with a suggestion for general practice, "One term must always be reduced to have the same coefficient, and then the difference between the numbers is necessarily the difference between the other term...." Today, this method of solving systems is called elimination. It leads us quite naturally to the notion of determinants. But first... Cramer!
In contrast to Cardano, Gabriel Cramer was an affable scholar. He is credited with the now infamous Cramer's Rule taught to lucky high school math students. However, the treatment given of his rule in high schools is appallingly distilled. We will look at his book Introduction A L'Analyse Des Lignes Courbes Algébrique to get the real story which follows Cardano's work. A partial translation into English can be found here.
*********************************************************
Consider the general 2 × 2 linear system
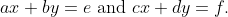
The method of elimination gives us the solution
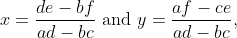
provided ad − bc is nonzero. Why is it necessary to say the denominator can't be zero? The numerators and denominator of the solution are commonly interpreted as something called a determinant. For a 2 × 2 matrix
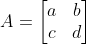
the determinant of A is denoted by det(A) or |A| and is given by
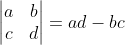
Now, let's look at the system of equations as the stack of equations
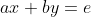
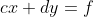
Notice that the numerators and denominators of the solution look like determinants of matrices. That is, we may write
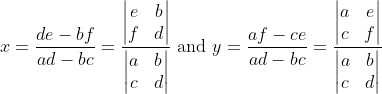
We see that the denominator of x and y is the determinant of a matrix C of the coefficients of the linear system. Furthermore, the numerator of x is the determinant of a matrix X we get by replacing the column of coefficients of x in C by the column of constants, and we define a matrix Y analogously. More precisely, let
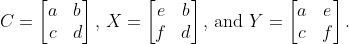
Thus, we may write the solution more elegantly as
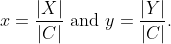
This formulation of the solution of a linear system into ratios of determinants is called Cramer's Rule. Its elegance allows us to solve 2 × 2 linear systems by mental calculation. Let's apply it to three different systems to see what else we may learn.
Example 1: Solve the system
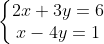
Solution: Three quick mental calculations tell us that
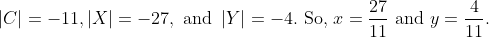
Example 2: Solve the system
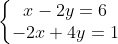
Solution: Immediately, we run into the problem of division by zero, for |C| = 0 and thus x and y are undefined. What does this mean about the system? A quick inspection of the slopes and intercepts of the lines described reveals why this system has no solution.
Example 3: Solve the system
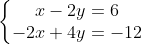
Solution: We run into the same problem of |C| = 0, but the slopes and intercepts of this system lead us to conclude that it has infinitely many solutions.
Naturally, we have some questions.
- Is the determinant of the coefficient matrix of a linear system being nonzero sufficient condition for the system to have a unique solution?
- Is it a necessary condition?
- What are the necessary and sufficient conditions for a linear system to have infinitely many solutions or have no solution?
- What do we mean by sufficient condition and necessary condition?
After enough practice using Cramer's Rule for 2 × 2 linear systems, we begin to notice that we can completely characterize their geometry in terms of the determinants of their matrices. How much practice is enough? That depends on who's asking. A 2 × 2 linear system describes
- two lines intersecting at a unique point if and only if |C| ≠ 0
- two parallel lines if and only if |C| = 0 and |X| ≠ 0, and
- one line if and only if |C| = 0 and |X| = 0.
If you don't understand this, it's because you haven't yet practiced enough. Keep at it and you will understand. But first, a word of caution... algebra hides the geometry of whatever it concerns itself with because it is designed to encode spatial relations. Thus, we must always bother to visualize the geometry being described by algebraic statements.
Another question arises. Can Cramer's Rule be generalized to solve n × n linear systems? Let's explore the solution of the general 3 × 3 linear system
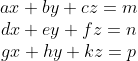
By eliminating z, we get the following reduction to the 2 × 2 linear system
x + (bf - ce)y = fm - cn \\ (dk - fg)x + (ek - fh)y = kn - fp \end{matrix})
The solution is given by Cramer's Rule:
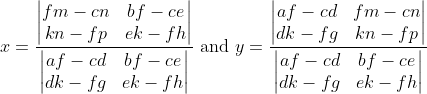
The determinants give us
(ek - fh) - (kn - fp)(bf - ce)}{(af - cd)(ek - fh) - (dk - fg)(bf - ce)} \text{ and } y = \frac{(af - cd)(kn - fp) - (dk - fg)(fm - cn)}{(af - cd)(ek - fh) - (dk - fg)(bf - ce)}.)
After distributing, alphabetizing factors, combining like terms, and cancelling the common factor, we get
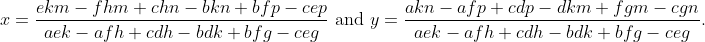
What a mess! Wouldn't it be beautiful if that mess turned out to be
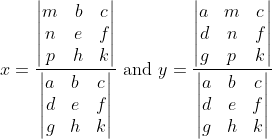
much like it is in the 2 × 2 case? To proceed, we will first have to return our attention to the definition of determinant because it's not yet clear how we may compute these 3 × 3 determinants. I will leave it to you to understand why we define determinants as we do since it usually proves to be a rather tedious exercise in solving linear systems. We could just proceed from the belief that whatever a determinant is, it is certainly based on the denominators of solutions of linear systems, a fact which led us to interpret the numerators as determinants as well. There also seems to be a recursive quality to solving the 3 × 3 system -- we reduced it to a 2 × 2 system -- so we may as well look for a similar recursion in exploring the determinant of a 3 × 3 matrix. Let's begin by noticing that some pairs of terms in the denominator of x have a common factor. Let's pretend for the moment that
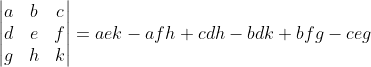
In terms of 2 × 2 determinants, we may write
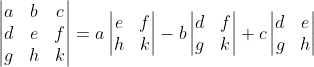
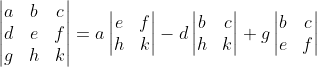
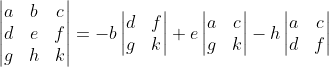
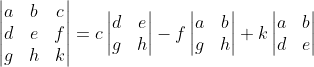
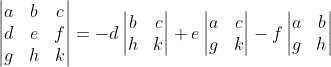
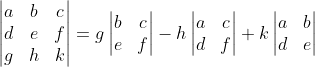
As it happens, there are only 6 distinct formulations of a 3 × 3 determinant into 2 × 2 matrices. Is there a counting formula for that? We shall see, but I digress. Back to the topic. Notice that each of these feature the entries in a single row or column, and each entry is multiplied by the determinant of the 2 × 2 matrix we get when the row and column containing that entry is excluded. For example, the entries of the determinant multiplied by a is found by removing the entries a, b, c found in the row of a and the entries d, g found in the column of a. That leaves the matrix
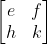
We call its determinant the minor of a, and we call a its cofactor. Through that lens, it is easy to see that each product in these 6 proposed formulations of the determinant of the coefficient matrix for the general 3 × 3 linear system contains a minor and its cofactor. Before we generalize this idea, we should take care to verify that a 2 × 2 determinant can also be characterized in this way. Have you convinced yourself? Great. Let's move on.
Question: What is the number of distinct expansions of an n × n determinant into (n − 1) × (n − 1) minors?
Recall that this exploration was dubious -- we pretended that 3 × 3 determinant was equivalent to the denominator of x. However, if we define the determinant of an n × n matrix to be precisely the denominator of the solution of the n × n linear system for which that matrix is the coefficient matrix, then we have defined a function on n × n matrices which seem recursively calculable as expansions into determinants of lesser dimension. We have determined this in the cases of 3 × 3 and 2 × 2 linear systems. There is, after all, nothing preventing us from doing just that. Why not run with it? We have this thing which comes out of the process of solving a linear system, and it turns out to be equivalent to a linear function of smaller such things we get from eliminating one variable from the original system. Yes, I am repeating myself because determinants are the intellectual equivalent of a briar patch: you can't get out without collecting more thorns.
Question: What effect does multiplication by a 2 × 2 matrix have on ℝ2 and can we classify those effects in terms of determinants?
Problem: Prove that the system
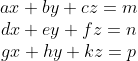
has solution
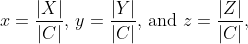
where

whenever |C| ≠ 0.
Let's try this on a famous example. By 100 BCE, the Chinese had posed and solved the following problem.
There are three types of corn, of which three bundles of the first, two of the second, and one of the third make 39 measures. Two of the first, three of the second and one of the third make 34 measures. And one of the first, two of the second and three of the third make 26 measures. How many measures of corn are contained by one bundle of each type?
MacTutor
There are three unknowns in this problem: the number of measures in one bundle of each type of corn.
Let x = the number of measures in one bundle of the first type.
Let y = the number of measures in one bundle of the second type.
Let z = the number of measures in one bundle of the third type.
This gives us the 3 × 3 linear system
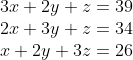
The Chinese solved this system using elimination on what they called a counting board. Thanks to European colonialism, that is now known as Gaussian Elimination on an augmented matrix. No, don't blame Gauss. Hate the game, not the player. Instead, we shall see whether the proposed extension of Cramer's Rule to the 3 × 3 case is useful. After setting up
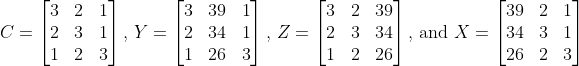
we see that |C| = 12 which tells us the system has a solution. Having a reason to proceed, we calculate |X| = 111, |Y| = 51, and |Z| = 33. So Cramer's Rule gives us
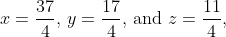
Questions: Were you able to obtain those fractions? Do they solve the system? If so, what does that tell us about determinants and Cramer's Rule? What is the geometry of 3 × 3 linear systems?
This determinant thing seems to be proving useful. Using elimination on a 2 × 2 system produces something we call a 2 × 2 determinant. Surprisingly, using elimination on a 3 × 3 linear system produces series of 2 × 2 determinants. Could it be that solving a 4 × 4 linear system will reveal a series of 3 × 3 determinants? I know I would rather not mess around with the general 4 × 4 case. The 3 × 3 case was messy enough. How about you? Perhaps there is a less tedious approach to exploring the generalization of determinants and Cramer's Rule.
We have already shown that the solution of a 3 × 3 linear system is computable in terms of 2 × 2 determinants that are evident from eliminating a variable to reduce the system to 2 linear equations in two unknowns. If we can somehow show that implies solutions of every system of higher order behave analogously, then we are in business. We will use a technique called mathematical induction which says that if a thing happens once, and that if it happening at all implies it will happen one more time, then it will happen every time. Well, that's the non-technical way of putting it. We shall be frighteningly technical from here on out. Suppose that

has solution
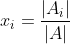
for |A| ≠ 0 and for each i from 1 to k, where A is the k × k coefficient matrix and Ai is the k × k matrix we get when the ith column of A is replaced with the column of constants d1 to dk. In other words, suppose that there is an integer k such that any k × k linear system has such solutions. Now, consider the system
}x_{k + 1} = f_{1} \\ b_{21}x_{1} + \cdots + b_{2(k + 1)}x_{k + 1} = f_{2} \\ \vdots \\ b_{(k + 1)1}x_{1} + \cdots + b_{(k + 1)(k + 1)}x_{k + 1} = f_{k + 1} \end{matrix})
Since we may reduce any (k + 1) × (k + 1) linear system to a k × k linear system by eliminating any one of its variables, say xk + 1, then there are coefficients cij and constants hi such that

is the reduction of our (k + 1) × (k + 1) linear system. By assumption, this reduced system has solution
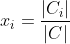
for |C| ≠ 0 and for each i from 1 to k, where C is the k × k coefficient matrix and Ci is the k × k matrix we get when the ith column of C is replaced with the column of constants h1 to hk. Substituting into the first equation of the (k + 1) × (k + 1) linear system gives us
}x_{k + 1} = f_{1})
which we may write as
} \left | C \right |})
It remains to show that
} \left | C \right |} = \frac{\left | B_{k + 1} \right |}{\left | B \right |})
where B is the (k + 1) × (k + 1) coefficient matrix of the (k + 1) × (k + 1) linear system and Bk + 1 is the (k + 1) × (k + 1) matrix we get when the (k + 1)th column of B is replaced with the column of constants f1 to fk + 1.
To finish this proof, we need a working definition of determinants for square matrices of any size. Looking back, we see that the determinant of an n × n matrix M is given by
^{i + j}M_{ij}m_{ij})
for a fixed integer i with 1 ≤ i ≤ n, where Mij is the ij entry of M and mij is its minor. We will show that this thing we are calling the determinant of an n × n matrix defines a unique function δ from ℝn × n to ℝ that satisfies
- δ(I) = 1.
- δ is linear in the rows of a matrix. In other words, if A, B, and D are n × n matrices, and Ai = cBi + c'Di, then δ(A) = cδ(Bi) + c'δ(Di).
- δ(A) = 0 whenever two adjacent rows of A are equal. [2]
I suppose I should hide this until I look up the proof, but where's the fun in that? I'll just leave it dangling loose. Maybe you'll figure it out before I do.
The Method of Gaussian Elimination on Augmented Matrices
Going back to the method of elimination, we see that we can safely do certain things to a system without altering its solutions. Given an m × n system of equations, we may interchange any two equations, scale an equation, or add an equation to the scalar multiple of another. Notice that each of those manipulations of a system of equations acts only to change the numbers in a row of its coefficient matrix augmented by the corresponding constant. Suppose A is the coefficient matrix and b is the column of constants. Then we call the matrix [A b] the augmented matrix of the system and we refer to the aforementioned actions on equations in the system as elementary row operations. It should be clear that the "counting board" used in Nine Chapters on the Mathematical Art is the augmented matrix of a 3 × 3 linear system, that elimination was performed by column operations analogous to the row operations we mentioned, and that substitution was used once the value of one variable was made explicit. However, if the contributors to Nine Chapters were to continue with column operations, the following augmented matrix would have been the result.
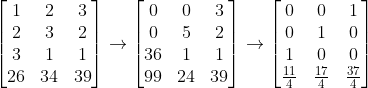
Today, we do practically the same thing, instead writing their first column as our first row, their second column as our second row, and their third column as our third row. Using row operations, we get

When considering why ancient Chinese mathematicians used column operations and solved for z first, we must keep in mind that they read and wrote in columns from top to bottom, then shifted left with each new column. However, we currently prefer to perform the row operations to solve for the leftmost variable. If, starting with the first row, we instead solved for x, then y, then z, we would see

In looking at the relative positions of the entries in the "counting board" and those in the augmented matrix, we are naturally led to the notion of the transpose of a matrix. For a matrix A, we denote its transpose by AT and define
_{ij} = A_{ji})
After a bit of investigation, it becomes clear that the Chinese mathematicians back in 100 BCE were merely operating on the transpose of the matrix we would use to solve the same problem. Thus, it seems that performing row operations on a linear system S with augmented matrix [A b] gives the same solutions as performing column operations on [A b]T. We may wonder what other properties of matrices are not affected by the transpose. For example, we may want to compare |A| and |AT| for all square matrices. Yes, we should. No, don't try. There is no try. Only do.
Oh, yeah, we almost forgot... Gaussian Elimination. There's not much to say really. No offense to the memory of Karl Friedrich Gauss -- he was one of the greatest mathematicians in history --, but all he did in this story was put his Enlightenment stamp of approval on what the Chinese did 2000 years before him.