Sometime in the 17 century BCE, some people living in the Fertile Crescent wrote on a clay tablet how to calculate the sum of numbers following some predictable patterns. They may have explored 1 + 2 + 3 + 4 + 5 + ... + 100, for example. Shall we?
Let's say S = 1 + 2 + 3 + 4 + 5 + ... + 100. We could certainly Google the answer or mindlessly keep adding until we get there, but what's the point in that? The point is to develop new skills and be the cleverest person in the room at parties. Let's look for patterns in the partial sums. What are partial sums? We may define the nth partial sum of S by
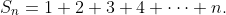
Then
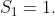
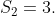
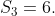
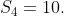
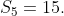
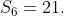

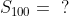
Are the partial sums revealing a way to calculate the 100th sum without rote? I don't think so either. Let's try breaking the problem into simpler parts. Notice that the sum we want is two smaller sums together: the odds + the evens. That is
 + (2 + 4 + 6 + 8 + \cdots + 100).)
Now, let's look at the partial sums of
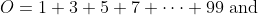
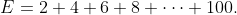
Denoting the nth partial sums of O and E by On and En, we may observe that
.)
Thus,
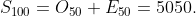
It must be noted that our reasoning so far is empirical. That is to say our final calculation is based on the prediction that things will keep happening as they have happened so far as we know. Thus, there is an unproved hypothesis afoot. However, our hypothesis suggests that
)
We still don't have an nth term formula for the case where the number of terms is odd. We could easily write it, but there is a better way to get at it. Consider that 2Sn = En . Therefore,
}{2})
If we take a different perspective on this result, we gain further insight. Writing it as
)
reveals to us that 1 + 2 + 3 + ... + n is the average of the first and last terms, multiplied by the number of terms. This is a common theme we will make use of later.
In mathematics, a series is such a sum of numbers where the problem is to be able to calculate it no matter how long it is.
In mathematics, a sequence is a list of things, like numbers or geometric figures. To understand the series above, we may form a sequence of partial sums.

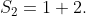
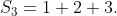
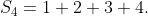

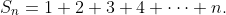
The sequence of partial sums for the series 1 + 2 + 3 + 4 + 5 + ⋯ is well-known and has a special name. Try to list them.
What are the next ten terms of the sequence?
To get the next ten partial sums, we must first determine the next ten terms in the series. After some observation, we see that each term in the series is one more than the last. In fact, we can write equations that relate each term to the previous. That is,

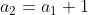
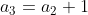
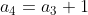

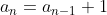
What is the 100th term of the sequence?
The equations above allow us to relate every term to the first. We begin by noting that
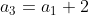
by means of a substitution. Furthermore, repeated substitutions give us
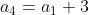
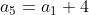

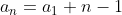
This last equation will tell us what the 100th term is without calculating all the terms between.
What is the nth term of the sequence?
What is the sum of the first n terms of the sequence?
What is the product of the first n terms of the sequence?
How to Analyze a Sequence
Suppose we have the sequence 7, 11, 15, 19, 23, 27, 31, 35, 39, ... and we want to know how the rest of the sequence will play out. We can analyze its structure in various ways. This is the opposite of producing a number that answers a question. What is called for is to dig and dig into the past until we find artifacts from the buried structure; we may also apply the analogy of chemical reagents to separate substances in a solution. The most important thing is to keep sleuthing until the mystery is solved.
To solve any problem, we must collect data and then look at it through various lenses.
Tabulation
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| an |
7 |
11 |
15 |
19 |
23 |
27 |
31 |
35 |
39 |
43 |
Numerical/Graphing
Colloquial Description
Complication/Unsimplifying/Structural Analysis/Reverse Engineering
Reformulation/Recursive Formulation/Explicit Formulation
Use the Scientific Method (or "Get Einstein on that bitch!}
Let's begin by supposing that there is a simple rule which generates the numbers in the sequence, a hypothesis if you will (hypothesize, experiment, observe, reason, question, repeat). Experiment 1: look at differences in consecutive terms: 4, 4, 4, 4, 4, .... Observations: Each number is 4 more than the previous. Conclusion 1: The sequence can be extended by simply adding 4 to the last number: 7, 7 + 4, 7 + 4 + 4, 7 + 4 + 4 + 4, .... Conclusion 2: Let an denote the nth term of the sequence; an = 7 + (n - 1)4.
Generally, when a sequence is generated by a common difference d, we have
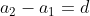
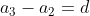
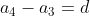
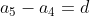

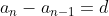
which gives us
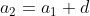
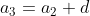
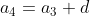
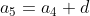

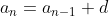
If we substitute the expression on the right side of each equation into the equation below it, then we see that
d)
A sequence in which the forward differences Δai = ai + 1 − ai are constant for all i, such as this one, we describe as arithmetic. When we want to add all the terms of sequence, we talk of a the series whose addends are the terms of the sequence. The sum of an arithmetic series is given by
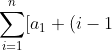d] = na_{1} + d\sum_{i = 1}^{n}(i - 1))
}{2})
d])}{2})
}{2})
This result is celebrated to be one of the oldest and most important theorems, here. The idea is to take the average of the first and last terms, then multiply the result by the number of terms. The Babylonians are credited with its first appearance, but they did not prove it. Having had no formal deductive edifice upon which to build proofs (that we know of), they probably did something like this (without the modern symbolism, of course).
If S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10, then 2S = 10(1 + 10). Therefore, S = 10(1 + 10) / 2.
If S = 7 + 11 + 15 + 19 + 23 + 27 + 31 + 35 + 39, then 2S = 9(7 + 39). Therefore, S = 9(11 + 39) / 2.
One wonders why the Babylonians concerned themselves with what seems like a very impractical problem. It certainly suggests there was an intellectual culture developing around mathematical calculations of the time. It is possible that this sort of puzzle found its way into parlor games, gambling and perhaps ultimatlely became child's play, which would explain how the formula would come to be a rule of thumb in a culture that did not concern itself with formal mathematical proof.
They may have even used counters or geometric representations to see the relations more clearly. Such would be a great way to guide students to reconstructing the formula for themselves.
Let's turn our attention to different sequence. The forward differences in 3, 6, 12, 24, 48, 96, 192, 384, ... are not constant. In fact, as we see, Δai = ai for all i. We will have to look at a different property: forward quotients. Let's define the forward quotient as follows. The forward quotient between two consecutives terms of a sequence is
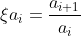
Notice that ξai = 2 for all i. This tells us that an = 3·2n − 1. We describe by geometric any sequence whose forward quotients are constant. More technically, a sequence of the form {arn} is called geometric. Let's consider the sum of a geometric series.
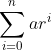
We begin with the simplest geometric series: 1 + 2 + 4 + 8 + 16 + 32 + ⋯ + 2n. If S = 1 + 2 + 4 + 8 + 16 + 32 + ⋯ + 2n, then 2S = 2 + 4 + 8 + 16 + 32 + 64 + ⋯ + 2n + 1. We see that S − 1 = 2S − 2n + 1.
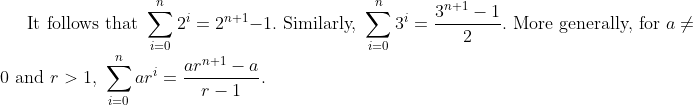
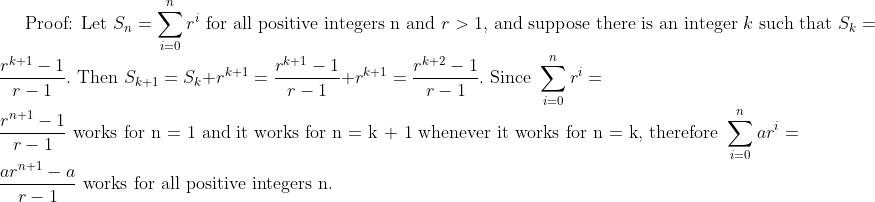
We have seen what happens when the forward differences of a sequence are either constant or reproduce the sequence itself. What if the forward differences of a sequence are arithmetic with common difference d? That is, suppose
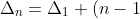d, \text { where } \Delta_{i} = \Delta a_{i}.)
By referring to those as first forward differences, we may define second forward differences in the following way.
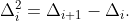
We see that
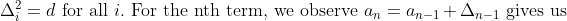
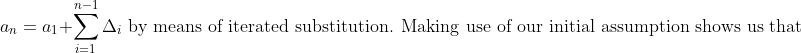
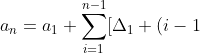d]. \text{ It is easy to show that this is a quadratic function in n, using only the first two terms of the sequence and the constant second forward difference. In particular,})
n + 2a_{1} - a_{2} + d.)
Let d be a constant. We have seen that
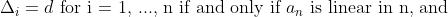
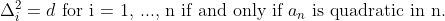
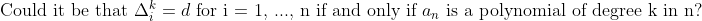
Let's take a look at the triangular numbers.
| n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| an |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
45 |
55 |
| Δn |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
--- |
| Δ2n |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
--- |
--- |
Theorem: For a sequence {an}, an is a quadratic in n if and only if Δ2i is constant for all i from 1 to n.
How to Analyze a Series
Partial Sums/Convergence/Special Functions